Nonlinear Dynamical Systems at SDSU
Dynamical Systems:
The Theory of Dynamical Systems is the paradigm for modeling and studying phenomena
that undergo spatial and temporal evolution. These phenomena range from simple
pendula to complex atomic lattices, from planetary motion to the weather system,
from population dynamics to complex biological organisms. The application of
Dynamical Systems has nowadays spread to a wide spectrum of disciplines including
physics, chemistry, biochemistry, biology, economy and even sociology.
In the past, modeling was mainly restricted to linear, or almost linear, systems
for which an analytical treatment is tractable. In recent years, thanks to the
advent of powerful computers and the Theory of Dynamical Systems, it is now
possible to tackle, at some extent, nonlinear systems. After all, nonlinearity
is at the heart of most of the interesting dynamics.
Sample Gallery:
As a taster for the kind of applications were Dynamical Systems is an indispensable
tool, we present the following gallery of problems. This constitute a sample
of topics where the members of our group have been successful in applying Dynamical
Systems ideas.
Choose from:
- Mathematical Physics
- Chaos
|
- Imaging
- Mathematical biology
|
To see a larger version for each image/film just click on it.
[If animations freeze try to refresh cache].
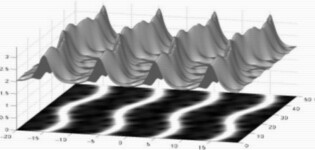 |
Interacting solitons in a chain of Bose-Einstein
condensates (BECs):
At ultra-cold temperatures dilute gasses turn into an exotic state called
Bose-Einstein condensate (BEC). BECs behave like macroscopic chunks of
quantum matter. The image on the left depicts vibrations of a chain of
BECs in a periodic optical trap. For this case all the solitons oscillate
in phase back and forth and up and down. If you check carefully, for each
left-right oscillation there are two up-down oscillations.
|
 |
Vortex arrays in Bose-Einstein condensates (BECs):
In two dimensions, a BEC accepts vortex-like solutions. These solutions
arise when a BEC is `stirred', producing radially symmetric kinks in the
field. By constructing the interaction potential between vortices, it
is possible to follow the dynamics of an array of interacting vortices.
An example is depicted on the left. [Click on the image to get an animation
of the vortex array interaction].
|
 |
Two colliding blobs of quantum matter:
In this two-component 3D setting, two drops of BECs each one initialized in
one of the components, interact. Both blobs are attracted towards the
center of the magnetic trap but, at the same time, they repel each other.
The interaction results on a periodic breathing of one blob tunelling through
the other one.
|
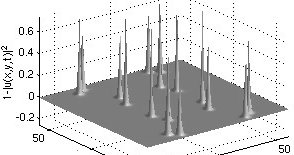
 |
Exponentially localized
oscillations (breathers) in a chain of BECs:
It is possible to prescribe an initial condition for a train of condensates
which evolves into a collective oscillation that is localized in space (top
image). The amplitudes of oscillation of the individual condensates decrease
exponentially away from the central condensate (x=0).
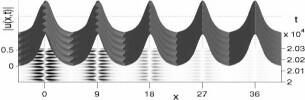
Homoclinic tangles:
The dynamics for the interacting condensates can be reduced to a two
dimensional map on the oscillation amplitudes of consecutive condensates.
The homoclinic tangle (bottom-left image) prescribes the amplitudes of oscillation
(bottom-right image) for the BEC breather (top image). The homoclinic tangle
reduction provides structural stability for the breather solution. |
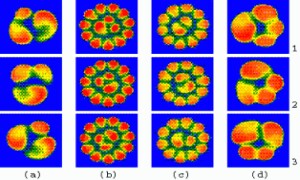 |
Hopping Patterns:
Experiments on a circular burner confirm that premixed gases burn irregularly,
causing a flame front to destabilize and form cellular patterns via symmetry-breaking
bifurcations. This example illustrates the spatio-temporal behavior of certain
patterns called "hopping states". These states are formed by cells that
sequentially make rapid changes of angular position while moving in a ring
structure. When an individual cell executes a hop, the other cells in the
ring remain symmetric and almost at rest. The ring can be isolated or can
be surrounded by a stationary ring, as is depicted in the composite picture.
Time evolves from top to bottom. [Click on the image to get an animation
of a hopping flame pattern]. |
|
|
Fluidization:
The fluidization phenomenon is the transport process of solid particles
by fluids, which, under certain conditions, can lead to the solids to
acquire fluid-like properties. In the attached animation we observe the
complex interaction between sand particles and gas in a fluidized bed.
The animations were created from numerical simulations of a model developed
by the National Energy and Technology Lab at the Department of Energy.
[Click on the image to trigger the animation].
|
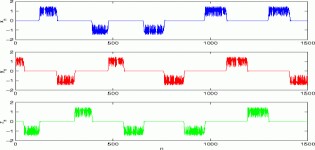 |
Cycling Chaos:
Cycling Chaos, in which solution trajectories cycle around symmetrically
related chaotic sets, is known to be a generic feature of coupled cell
systems modeled by continuous systems of differential equations with symmetry.
In related work, we demonstrated that cycling chaos can also be a generic
feature of discrete Dynamical Systems governed by difference equations.
The accompanying picture on the left shows simulation results of a network
with three cells. The internal dynamics of each cell is modeled by a cubic
map with local reflectional symmetry. Observe that at any given time,
one cell is active while the others are quiescent.
|
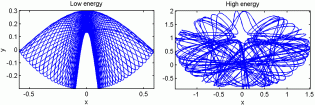 |
Transition to Chaos:
Some systems behave regularly in a predictable fashion for low energies
(left panel). However, when the energy is increased beyond a certain threshold,
the orbits may become chaotic (right panel). Such change in behavior is
called an order-to-chaos transition. The orbits on the left represent
an extensible pendulum (pendulum with a spring). It turns out that by
careful analysis of the potential energy it is possible to estimate the
energy where the chaos-order transition occurs.
|
   |
PDE-based
Methods for Image Restoration
The image sequence shows the initial image, the degraded (noisy) image,
and the image recovered after reconstruction with the total variation norm.
Some of the most successful PDE-based restoration algorithms are based on
the total variation (TV) norm. The restoration is obtained by minimization
of the TV functional, subject to constraints which relate the solution to
the measured image, and the noise level. |
 |
Time-reversal
and Imaging in Random Media
In time-reversal acoustics a signal is recorded by an array of
transducers, time-reversed and then retransmitted into the medium. The retransmitted
signal propagates back through the same medium and refocuses approximately
on the source. The possibility of refocusing by time-reversal has many important
applications in medicine, geophysics, non-destructive testing, underwater
acoustics, wireless communications, etc.
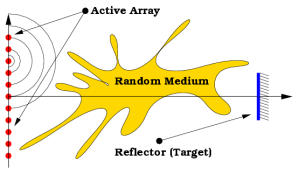
In Imaging (see figure) the target is illuminated by transmissions
from the array of transducers, the echo (response) is recorded, and then
the problem is to figure out where the target was located, its size, etc.
|
 |
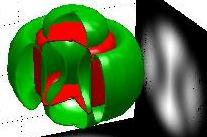
Aggregation and Metastability:
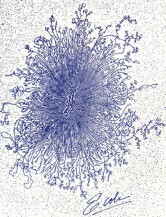
The animation on the left represents the interaction of two aggregates
(red) of cells via a chemo-attractant (green). The cells produce the chemo-attractant
which in turn attracts more cells leading to "humps" (aggregates)
of cells. This chemically driven aggregation, or chemotaxis, is believed
to be behind the formation of senile plaques leading to Alzheimer disease.
Aggregates typically interact with other aggregates on exponentially large
times (metastability). This slow interaction (check carefully the clock)
is due to the exponentially small overlap of the tails for neighboring aggregates.
The mathematical treatment of such interactions is nontrivial and standard
asymptotic or perturbation techniques usually fail. [Click the image to
get a larger view of the animation] |
  |
Modeling Cellular
Control Systems:
One of the important questions, which scientists are currently investigating,
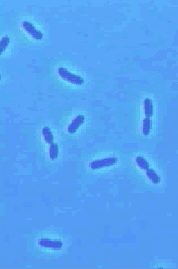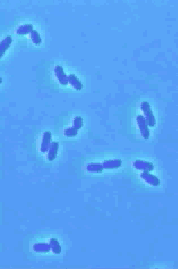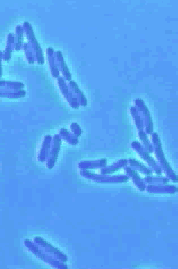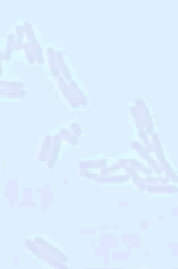
concerns how the cell cycle begins in bacterial cells. Using information
that is known about the biochemical processes in Escherichia coli (see images
on the left) may help to try to determine the key controlling steps in the
initiation of DNA replication. From a modeling perspective, it is important
to examine several aspects of growing cultures of bacterial cells using
biochemical kinetics to study cellular control problems from a theoretical
perspective. It is hoped that these studies will assist the experimental
studies in discovering the most significant steps initiating the cell cycle.
[Click on the images to see a larger versions]. |
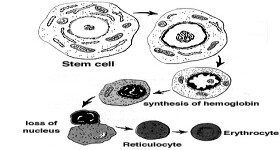 |
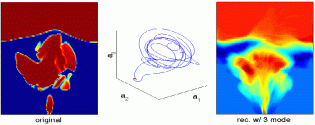
Age-Structured Models for Erythropoiesis:
Age-structured models for the development of mature red blood cells, or
erythropoiesis (see left image), began as an inquiry into the relation
between complicated age-structured models to the significantly simpler
systems of delay differential equations. Some models for hematopoiesis
have interesting results for both hematopoietic (blood) diseases and the
mathematical analysis of state-dependent delay differential equations.
Recent work has shown how the variable velocity of aging in erythropoiesis
can stabilize the mathematical model.
|
This page has been accessed  times since February 2002.
times since February 2002.
Last update: 20 March 2002.
Maintained by
Ricardo Carretero
Ricardo Carretero Gonzalez
Antonio Palacios Peter Blomgren Joe Mahaffy Diana Verzi Chris Curtis San Diego
San Diego State University SDSU California West coast MS master
masters PhD doctorate doctoral graduate undergraduate concentration
emphasis applied mathematics chaos chaotic fractal fractals dynamics
dynamical systems nonlinear nonlinear dynamical systems nonlinear
dynamics NLDS model modeling modelling publication publications
research preprints analysis adaptivity aggregation bifurcation
bifurcations bioloby blowup blow up blow-up bose bose-einstein
breather breathers CML CMLs condensates coupled map lattices delay
differential determinism deterministic differential einstein embedding
equation equations fluidization fluidized GPE heteroclinic homoclinic
ILM ILMs image restoration intrinsic localized modes lattices
manifold map maps math mathematical bioloby metastability moving
mesh NLS nonlinear waves numerics numerical ODE ODEs orbit orbits
pattern patterns PDE PDEs POD prediction proper orthogonal decomposition
reconstruction soliton solitons spatio temporal stable stochastic
studies study systems tangle temporal time series unstable
|