Recently Andreas Strombergsson of Bristol University, UK, asked me about the
asymptotics of the W Whittaker confluent hypergeometric function. This W
function can be expressed in terms of the famous U confluent
hypergeometric function. The desired asymptotic results are required for
obtaining bounds on certain sums of the Fourier coefficients of Maass Wave
eigenfunctions, and also for estimates on the equidistribution of non-closed
horocycles on non-compact surfaces. The W function has two parameters  and
and 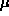 , along with a dependent variable x. The asymptotics he
asked for are non-trivial! Namely, he wants , along with a dependent variable x. The asymptotics he
asked for are non-trivial! Namely, he wants  purely imaginary with purely imaginary with 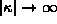 , uniformly for , uniformly for 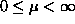 as well as for as well as for 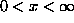 . I show how such results can be obtained
using a general asymptotic theory from O.D.E.s that I obtained at SDSU in
1990. In this application it is necessary to take x into the complex plane. . I show how such results can be obtained
using a general asymptotic theory from O.D.E.s that I obtained at SDSU in
1990. In this application it is necessary to take x into the complex plane.
|